Chapter 2 Introducing the likelihood function
We will often work with continuous rather than discrete random variables, so we would use the probability density function instead of the probability mass function. The theory in this case is very similar, so it is common to use the same notation in both cases.
Let \(X\) be a random variable, whose distribution depends on some unknown parameter \(\theta\). Let \(x\) be the observed value of \(X\).
We now write \(f(x; \theta)\) to represent either the probability density function \(f_X(x)\) if \(X\) is continuous, or the probability mass function \(p_X(x)\) if \(X\) is discrete, where \(f_X(x)\) (or \(p_X(x)\)) is evaluated at the observation \(x\).
We denote the set of possible values of \(\theta\) by \(\Theta\), and define the likelihood function as follows.
Definition 2.1 (likelihood function)
The likelihood function of \(X\), given the data \(x\), is \(L:\Theta\to\mathbb{R}\) defined by
\[L(\theta; x)=f(x;\theta)\]
We refer to the value of \(L(\theta;x)\) as the likelihood of \(\theta\) given the data \(x\). Think of the likelihood as the probability or density of the observed data, expressed as a function of \(\theta\).
The likelihood is thought of as function of the unknown parameter \(\theta\). The observed data \(x\) is known, so any instance of \(x\) in the function \(L(\theta; x)\) will be replaced by a number. Note that viewed as a function of \(\theta\), the likelihood is not a probability density function. For example, it typically will not integrate over \(\Theta\) to give \(1\).
The (hopefully unique) \(\theta\in\Theta\) which maximises \(L(\theta; x)\) is known as the maximum likelihood estimator of \(\theta\). We usually denote it by \(\widehat\theta\).
Sometimes, we will refer to the likelihood function of a distribution; this is the likelihood function of a random variable with that distribution. The process of finding the maximum likelihood estimator \(\hat\theta\) is known as maximum likelihood estimation.
Example 2.1 (Likelihood functions and maximum likelihood estimators)
Let \(X\) be a random variable with \(Exp(\theta)\) distribution, where the parameter \(\theta\) is unknown. Find the and sketch the likelihood function of \(X\), given the data \(x=3\).
Solution
The likelihood function is \[L(\theta; 3)=f(3;\theta)=\theta e^{-3\theta}\] defined for all \(\theta\in\Theta=(0,\infty)\). We can plot this in R, for \(\theta\in(0,4)\)
curve(x*exp(-3*x), from = 0, to = 4,
xlab=expression(theta),
ylab=expression(L(theta~";"~3)))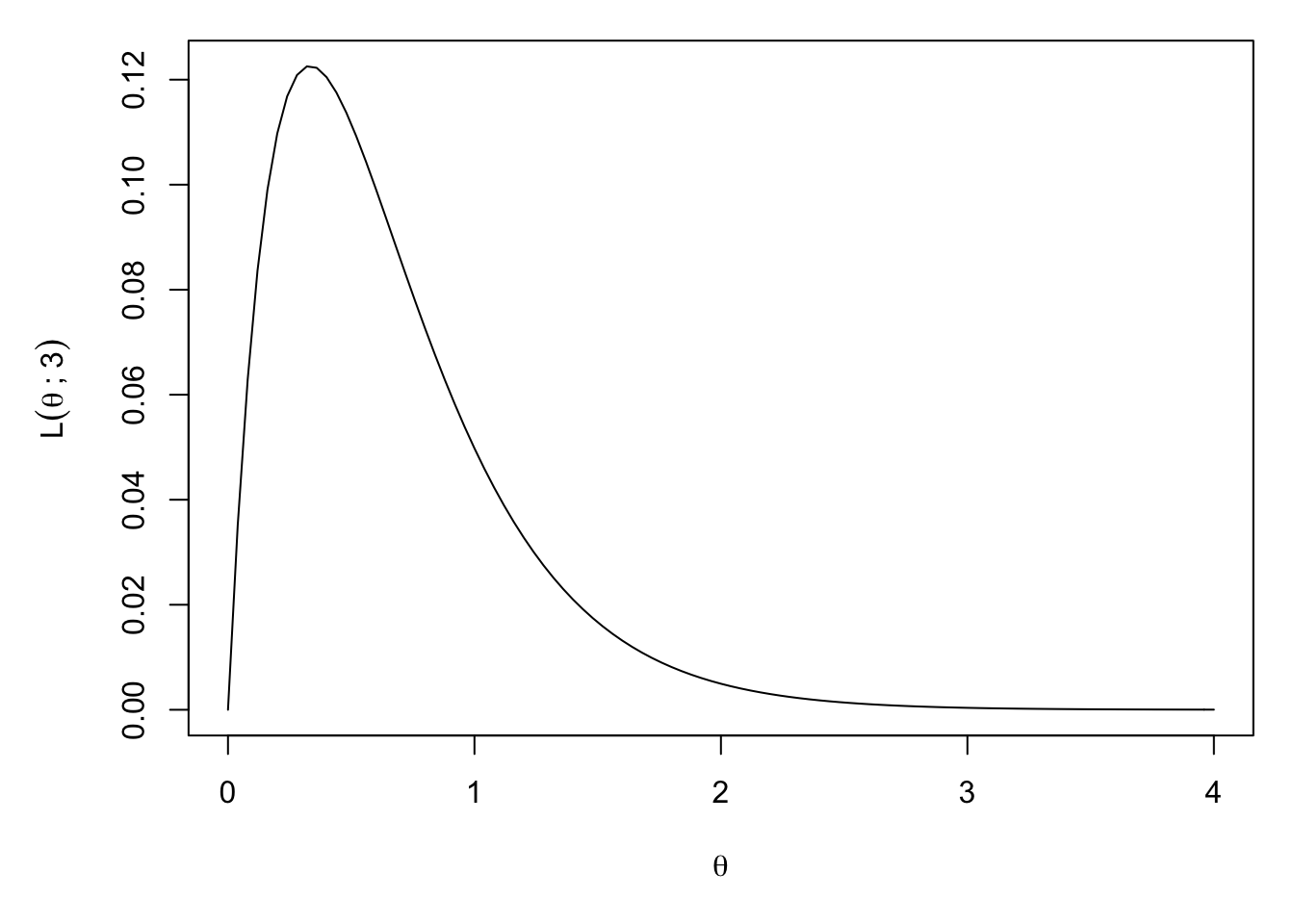
(Note that we use x as the \(\theta\) variable here because R hard-codes its use of x as a graph variable in the curve() function.)
Given this data, find the likelihood of \(\theta=\frac{1}{10},\frac12,1,2,5\). Amongst these values of \(\theta\), which has the highest likelihood?
Solution
The likelihoods are \[\begin{alignat*}{2} L(\tfrac{1}{10};3)&=\tfrac{1}{10}e^{-\frac{3}{10}}&&\approx 0.07\\ L(\tfrac12;3)&=\tfrac12e^{-\frac32}&&\approx 0.11\\ L(1;3)&=1e^{-3}&&\approx 0.05\\ L(2;3)&=2e^{-6}&&\approx 0.005\\ L(5;3)&=5e^{-15}&&\approx 1.5 \times 10^{-6}\\ \end{alignat*}\] So, restricted to looking at these values, \(\theta=\frac12\) has the highest likelihood.
Find the maximum likelihood estimator of \(\theta\in(0,\infty)\), based on the (single) data point \(x=3\).
Solution
We need to find the value of \(\theta\in\Theta\) which maximises \(L(\theta;3)\). We differentiate, to look for turning points, obtaining \[\begin{align*} \frac{dL}{d\theta} &=e^{-3\theta}-3\theta e^{-3\theta}\\ &=e^{-3\theta}(1-3\theta). \end{align*}\] Hence, there is only one turning point, at \(\theta=\frac13\). We differentiate again, obtaining \[\begin{align*} \frac{d^2L}{d\theta^2} &=-3e^{-3\theta}(1-3\theta)+e^{-3\theta}(-3)\\ &=e^{-3\theta}(-6+9\theta) \end{align*}\] At \(\theta=\frac13\), we have \(\frac{d^2L}{d\theta^2}=e^{-1}(-6+3)<0\), so the turning point at \(\theta=\frac13\) is a local maximum. Since it is the only turning point, it is also the global maximum. Hence, the maximum likelihood estimator of \(\theta\) is \(\hat\theta=\frac13\).
The value \(\hat\theta\) which maximises \(L(\theta; x)\) changes if we use a different value for \(x\). This is natural - the choice of parameters that we think is best, depends on the data that we have.