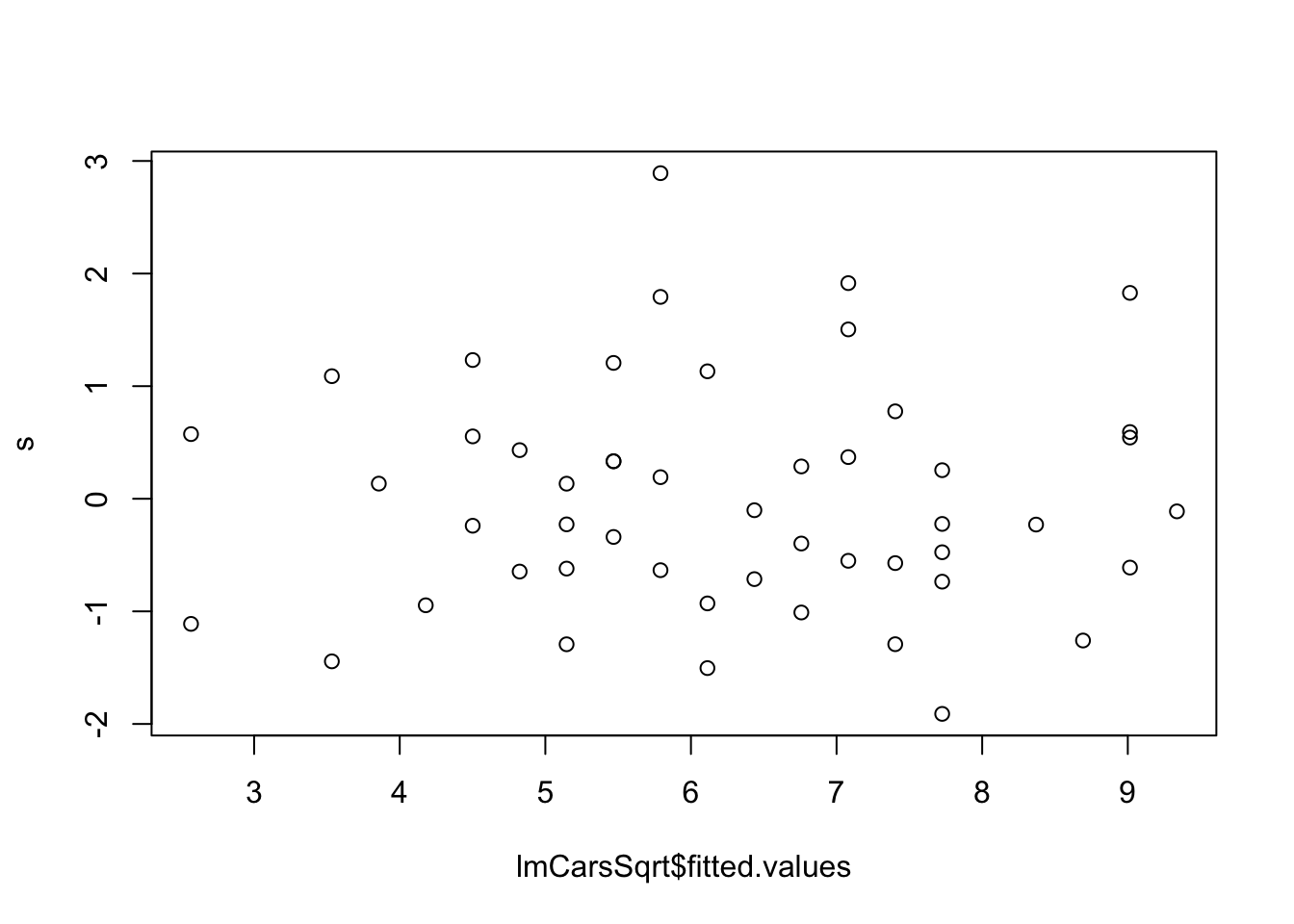
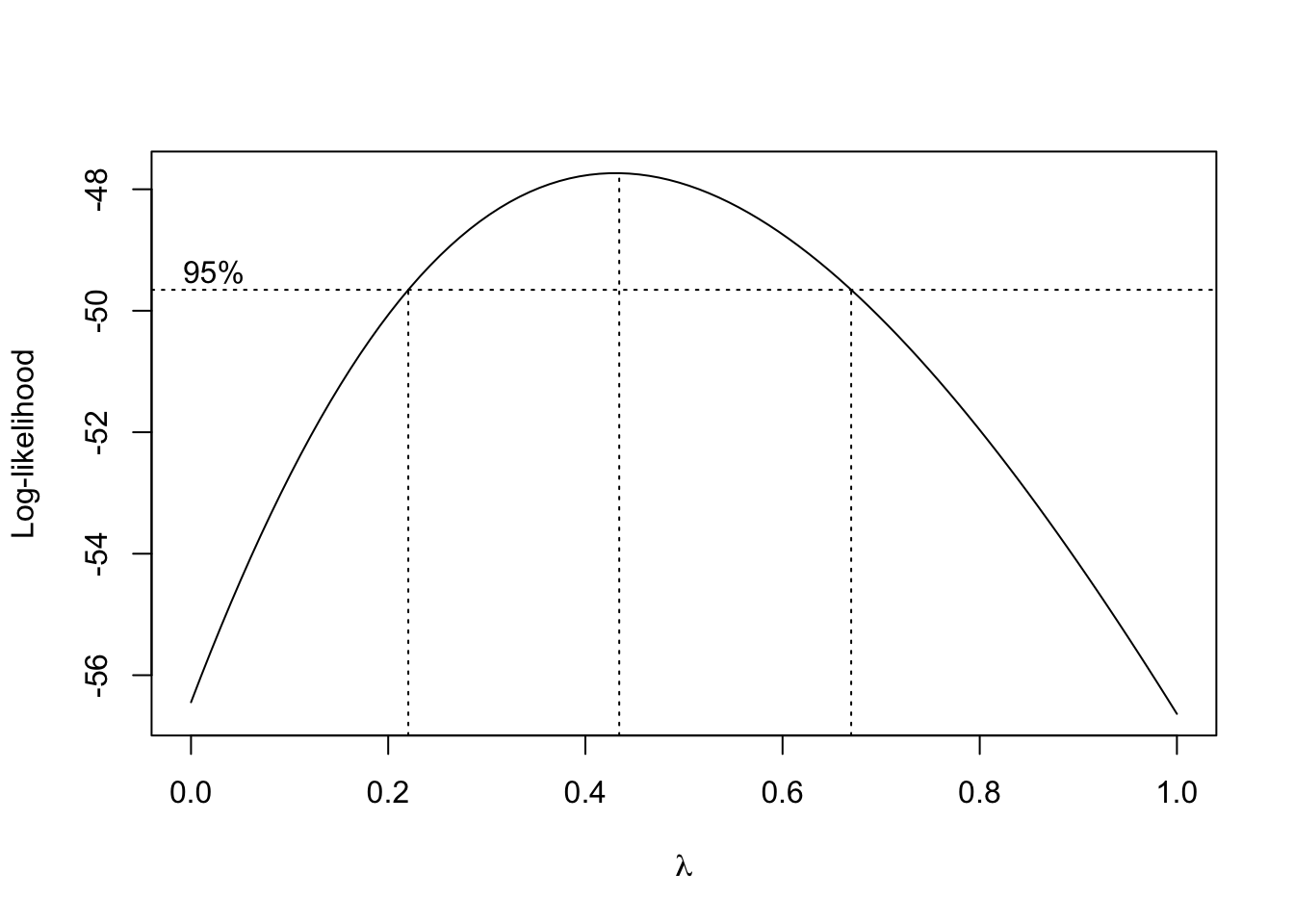
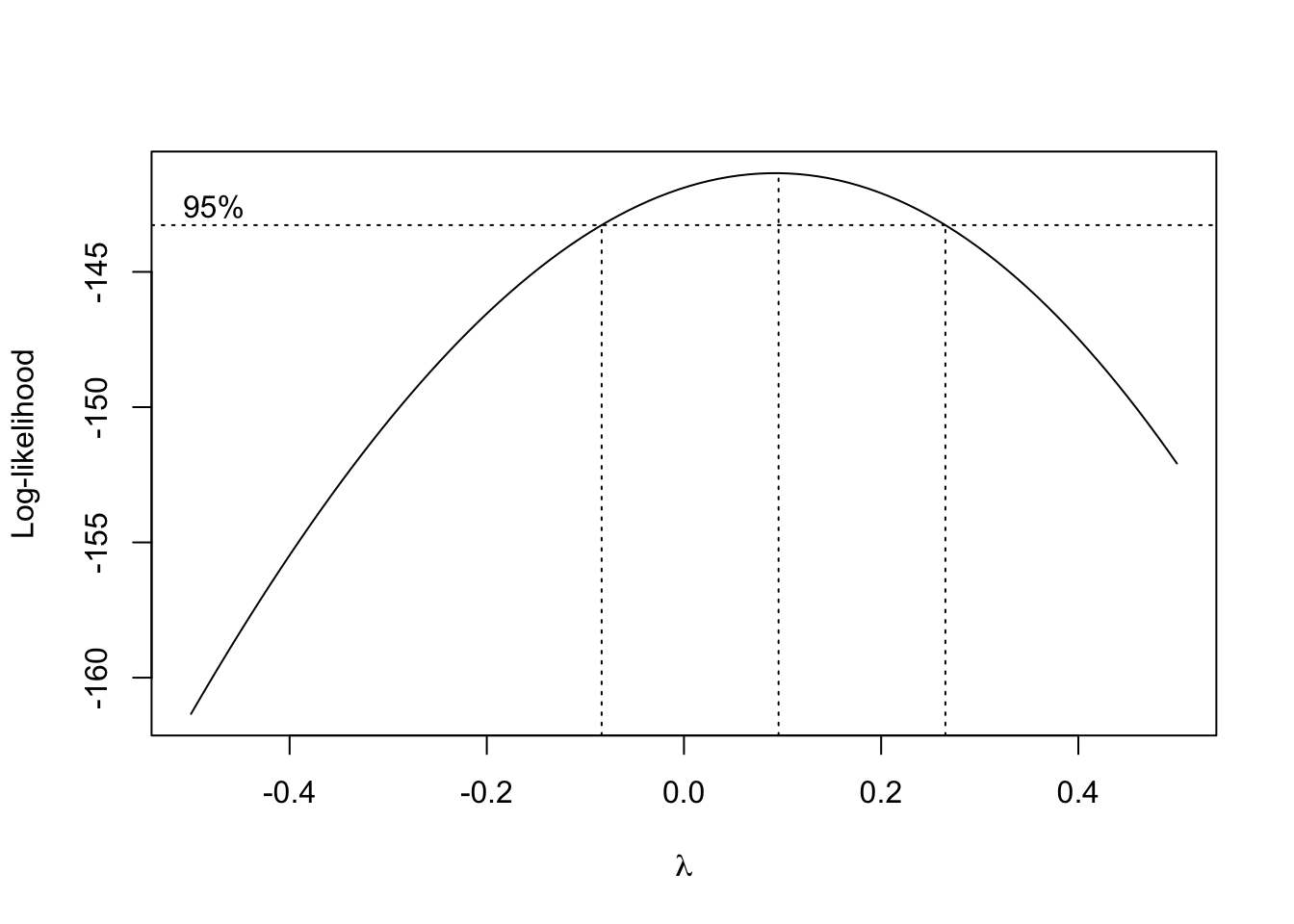
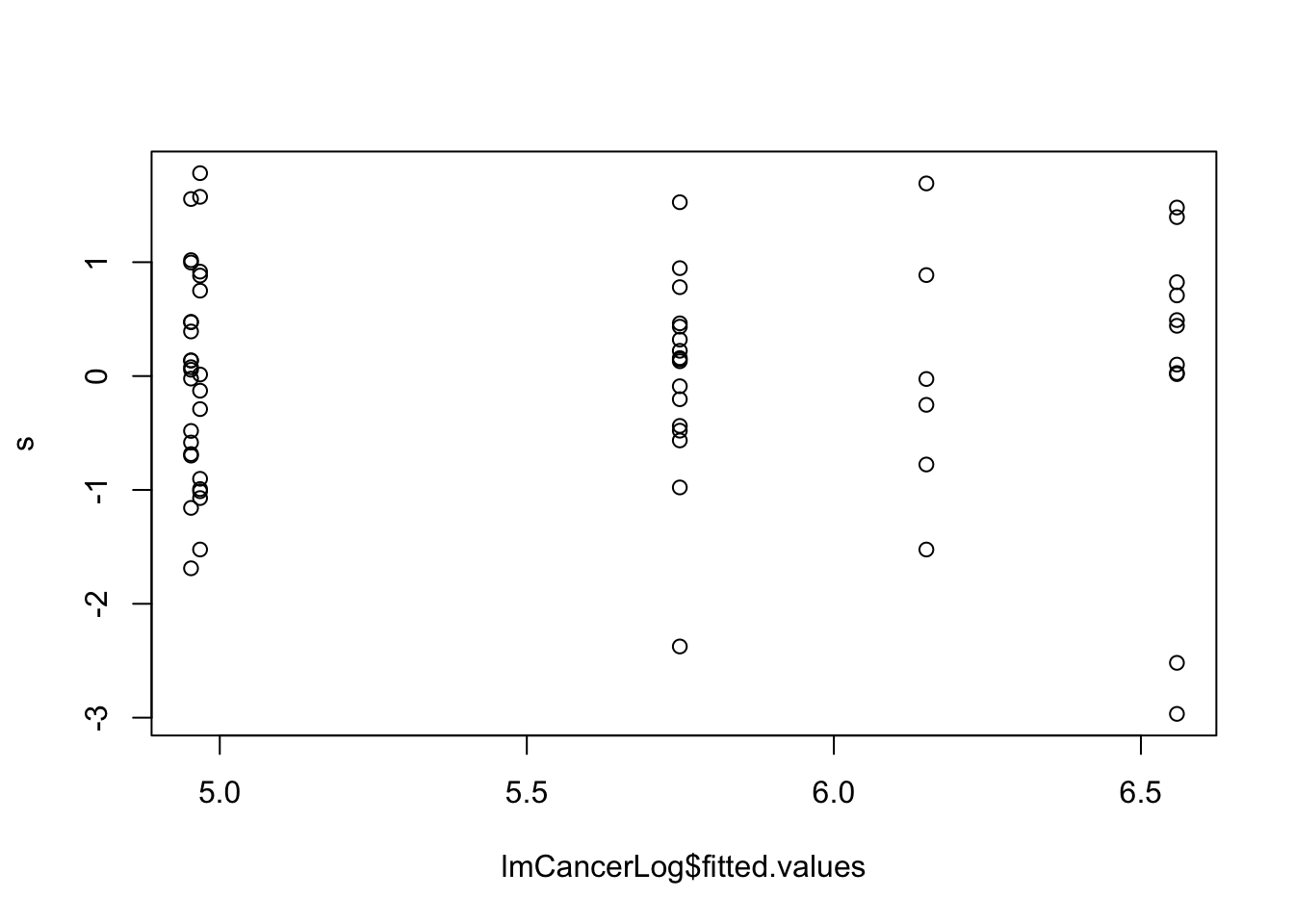
lmCars <- lm(dist ~ speed, cars)
anova(lmCars)Analysis of Variance Table
Response: dist
Df Sum Sq Mean Sq F value Pr(>F)
speed 1 21186 21185.5 89.567 1.49e-12 ***
Residuals 48 11354 236.5
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1